12.03
2017年12月3日 難問
難問に遭遇した。
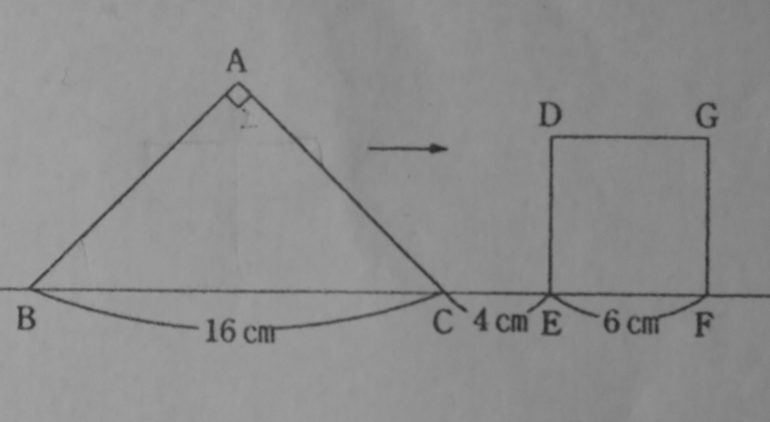
アイキャッチ画像にした図形である。これ、左の直角二等辺三角形が秒速2cmで右に進む。やがて右にある正方形と重なる。
ここからが問題で、重なった部分の綿世紀が最大となるのは何秒後か、その時の面積は、というものだ。
この問題で引っかかってしまった。
面積が最大? どこで最大になる?
これ、2次関数を使えば簡単に出る。重なった時、正方形の一部ははみ出して、三角形の外に出る。そのはみ出し三角形もやはり直角二等辺三角形になり、1個しかはみ出しができなくても2個になっても、辺の合計は2cmになる。
だから、2つの二等辺直角三角形の短い辺をa、b(1個の場合はどちらかが0)とすると、
a+b=2
このはみ出し三角形の面積が最小になった時、重なった部分の面積は最大になるので、このはみ出し三角形の面積を求める。
面積=a2+b2/2
である。
この2つの式から
面積=a2-2a+2
=(a-1)2+1
である。面積はaが1の時もっとも小さくなり、はみ出し三角形の面積はこのとき1になる。
まあ、
「直感的にも、正方形が真ん中に来た時だよな」
と分かるのだが、
「見れば分かるだろ、真ん中だって」
というのは、算数の道に外れる。算数とは、数学とは、厳密な論理に縛られるのである。直感は排除せねばならない。
じゃあ、この問題、小学生にどう教えたらいい? 2次関数の最大・最小で説明しても理解してもらえるはずがない。
実はこれ、瑛太の塾のテキストに掲載されている。瑛太に算数を教える必要から、先に解いておこうと取り組んだ。ところが、小学生の知識範囲での解き方が分からないのである。
困った。
四日市の啓樹にSOSを出した。啓樹はいま中学1年生。瑛太と年齢が近いし、小学生の時からこちらも塾通いしているので、小学算数の範囲での解き方を知っているのではないかと期待したのである。
何しろ私は、自慢ではないが、小学校、中学校とほとんど勉強した記憶がない。自宅での勉強なるものに目覚めたのは高校2年生の夏休みである。算数、数学の知識は、それ以降に獲得したものがほとんどだ。小学校の「鶴亀算」なんて、
「どうして方程式で解かないんだ?」
というばかりで、いまだに頭をひねらないと鶴亀算では解けない体たらくである。
が、小学校の頃からきちんと勉強してきた啓樹なら分かるのでは?
が、だ。今のところ啓樹もできない。昨日の朝は、私がまだ夢から覚めないうちに電話をかけてきて
「できたよ」
と話し始めたのだが、
「ん、それで小学生に説明できるか?」
と突っ込むと
「そうか」
という状態である。
桐生で、小学生、中学生相手に無料で算数を教えている知人にもファックスでこの問題を送り、指導を願った。先週末のことである。いまだに返答が来ないということは、彼も私と同じ壁にぶつかっているのか。
これは私の精神衛生上、極めて良くない状態である。気になって仕方がないのだ。小学生に説明可能な解き方はないか?
「あんた、意外にアホやな。こんな簡単な問題が出来ひんとは、誠に持って情けない」
と呆れていらっしゃるあなた。よろしければメールで解き方を教えていただけませんか? 謝礼までは考えておりませんが……。
今日は、啓樹と嵩悟がピアノの発表会に臨んだらしい。facebookで2人の演奏に接した。
啓樹は3年連続のトリを努めたそうだ。弾いたのはラフマニノフ。
「ラフマニノフ? よくそんな曲知ってたな」
と電話で驚いたら、浅田真央ちゃんがアイスダンスで使ってポピュラーになった曲なのだそうだ。
啓樹、嵩悟とも、なかなかみごとにピアノを弾きこなしていたことを付け加えておきたい。


